정렬
선택 정렬
정렬되지 않은 원소들 중 가장 작은 원소를 찾아 가장 앞의 원소와 교환하는 알고리즘

이미지 출처 : https://gyoogle.dev/blog/algorithm/Selection%20Sort.html
방법
각 루프마다
- 최대 원소를 찾는다
- 최대 원소와 맨 오른쪽 원소를 교환한다
- 맨 오른쪽 원소를 제외한다
하나의 원소만 남을 때까지 반복
public void selectionSort(int[] arr) {
int minIdx;
int temp;
for(int i = 0; i < arr.length - 1; i++) {
minIdx = i;
for (int j = i + 1; j < arr.length; j++) {
if(arr[j] < arr[minIdx]) {
minIdx = j;
}
}
temp = arr[minIdx];
arr[minIdx] = arr[i];
arr[i] = temp;
}
}
시간 복잡도
- 최선 : O(n^2)
- 평균 : O(n^2)
- 최악 : O(n^2)
버블 정렬
서로 인접한 두 원소를 비교하여 정렬하는 알고리즘
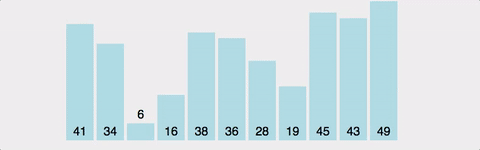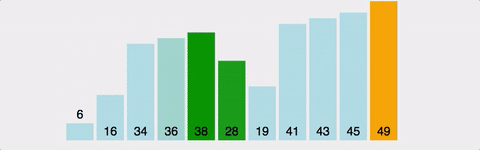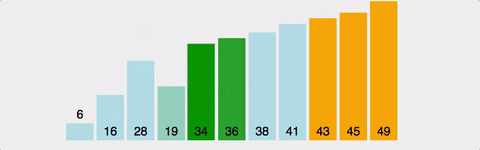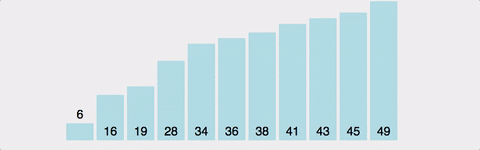
이미지 출처 : https://gyoogle.dev/blog/algorithm/Bubble%20Sort.html
방법
각 루프마다
- n번째 원소가 n+1번째 원소보다 크면 서로 교환한다
- 맨 오른쪽 원소를 제외한다
하나의 원소만 남을 때까지 반복
public void bubbleSort(int[] arr) {
int temp;
for(int i = 0; i < arr.length; i++) {
for(int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
}
}
}
}
시간 복잡도
- 최선 : O(n^2)
- 평균 : O(n^2)
- 최악 : O(n^2)
삽입 정렬
모든 원소를 이미 정렬된 배열을 앞에서부터 차례대로 비교하여 자신의 위치에 삽입하는 알고리즘

이미지 출처 : https://gyoogle.dev/blog/algorithm/Insertion%20Sort.html
방법
두 번째 원소부터 선택하여 각 루프마다
- 이전 위치의 원소가 선택한 값보다 크면 서로 교환하고 더 이전 위치를 가리키고 반복한다
- '1'번 반복이 끝나면 현재 가리키는 원소의 다음 위치에 선택한 원소를 삽입한다
하나의 원소만 남을 때까지 반복
public void insertionSort(int[] arr) {
int temp;
for(int i = 1; i < arr.length; i++) {
temp = arr[i];
int j;
for(j = i - 1; j >= 0 && arr[j] > temp; j--) {
arr[j + 1] = arr[j];
}
arr[j + 1] = temp;
}
}
시간 복잡도
- 최선 : O(n)
- 평균 : O(n^2)
- 최악 : O(n^2)
병합 정렬
큰 문제를 작은 문제 단위로 쪼개면서 해결하는 알고리즘

이미지 출처 : https://medium.com/@bill.shantang/8-classical-sorting-algorithms-d048eec3fdabl
방법
- 정렬한 배열을 2등분하여 왼쪽 오른쪽으로 나눈다
- 왼쪽 배열을 정렬한다
- 오른쪽 배열을 정렬한다
- 두 배열을 가지고 대소비교하여 임시 배열에 정렬한다
- 임시 배열을 기존 배열에 복사한다
public void merge(int[] arr, int left, int middle, int right) {
int i = left;
int j = middle + 1;
int idx = 0;
int k;
int[] list = new int[right + 1];
while(i <= middle && j <= right) {
if(arr[i] <= arr[j]) {
list[idx] = arr[i];
i++;
idx++;
}
else {
list[idx] = arr[j];
j++;
idx++;
}
}
if(i > middle) {
for(k = j; k <= right; k++) {
list[idx++] = arr[k];
}
}
else {
for(k = i; k <= middle; k++) {
list[idx++] = arr[k];
}
}
idx = 0;
for(k = left; k <= right; k++) {
arr[k] = list[idx++];
}
}
public void mergeSort(int[] arr, int left, int right) {
int middle;
if(left < right) {
middle = (left + right) / 2;
mergeSort(arr, left, middle);
mergeSort(arr, middle + 1, right);
merge(arr, left, middle, right);
}
}
시간 복잡도
- 최선 : O(nlog2n)
- 평균 : O(nlog2n)
- 최악 : O(nlog2n)
퀵 정렬
분할 - 정복 - 결합 과정을 통해 원소들을 정렬하는 알고리즘

이미지 출처 : https://gyoogle.dev/blog/algorithm/Quick%20Sort.html
방법
- 배열 가운데에서 하나의 원소를 골라 pivot이라 칭한다
- 배열 내부 모든 원소들을 검사하며 pivot보다 작은 원소들은 왼쪽에 큰 원소들은 오른쪽에 배치한다
- 생성된 두 개의 배열 각각에 새로운 pivot을 만들어 다시 쪼갠다
- 더 이상 쪼갤 수 없을 때까지 진행한다
public void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public int partition(int[] arr, int left, int right) {
int pivot = arr[left];
int i = left;
int j = right;
while(i < j) {
while(pivot < arr[j]) {
j--;
}
while(i < j && pivot >= arr[i]){
i++;
}
swap(arr, i, j);
}
arr[left] = arr[i];
arr[i] = pivot;
return i;
}
public void quickSort(int[] arr, int left, int right) {
if(left >= right)
return;
int pivot = partition(arr, left, right);
quickSort(arr, left, pivot-1);
quickSort(arr, pivot+1, right);
}
시간 복잡도
- 최선 : O(nlog2n)
- 평균 : O(nlog2n)
- 최악 : O(n^2)
힙 정렬
완전 이진 트리를 기반으로 하는 힙으로 정렬하는 알고리즘
방법
- 최대 힙을 구성한다
- 현재 힙 루트의 가장 큰 값을 루트의 마지막 원소와 바꾼 후 크기를 하나 줄인다
- 힙의 크기가 1보다 크면 위 과정을 반복한다
public void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public void heapSort(int[] arr) {
int n = arr.length;
for (int i = n / 2 - 1; i >= 0; i--){
heap(arr, n, i); // 1
}
for (int i = n - 1; i > 0; i--) {
swap(arr, 0, i);
heap(arr, i, 0);
}
}
public void heap(int[] arr, int n, int idx) {
int p = idx;
int left = idx * 2 + 1;
int right = idx * 2 + 2;
//왼쪽
if (left < n && arr[p] < arr[left]) {
p = left;
}
//오른쪽
if (right < n && arr[p] < arr[right]) {
p = right;
}
//부모노드 < 자식노드
if(idx != p) {
swap(arr, p, idx);
heap(arr, n, p);
}
}
시간 복잡도
- 최선 : O(nlog2n)
- 평균 : O(nlog2n)
- 최악 : O(nlog2n)
기수 정렬
낮은 사리수부터 비교하여 정렬하는 알고리즘

이미지 출처 : https://medium.com/@bill.shantang/8-classical-sorting-algorithms-d048eec3fdab
방법
- 0~9까지의 bucket을 만든다
- 모든 원소들에 대하여 가장 낮은 자리수에 해당하는 bucket에 차례대로 원소를 둔다
- 0부터 차례대로 bucket에서 데이터를 다시 가져온다
- 가장 높은 자리수를 기준으로 하여 자리수를 높여가며 반복한다
public int getMax(int[] arr, int n) {
int max = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
return max;
}
public void countSort(int arr[], int n, int exp) {
int[] buffer = new int[n];
int[] count = new int[10];
int i;
// exp의 자릿수에 해당하는 count 증가
for (i = 0; i < n; i++){
count[(arr[i] / exp) % 10]++;
}
// 누적합 구하기
for (i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// 일반적인 Counting sort 과정
for (i = n - 1; i >= 0; i--) {
buffer[count[(arr[i]/exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
for (i = 0; i < n; i++){
arr[i] = buffer[i];
}
}
public void radixsort(int arr[], int n) {
// 최댓값 자리만큼 돌기
int m = getMax(arr, n);
// 최댓값을 나눴을 때, 0이 나오면 모든 숫자가 exp의 아래
for (int exp = 1; m / exp > 0; exp *= 10) {
countSort(arr, n, exp);
}
}
시간 복잡도
- 평균 : O(d * (n + b))
- d는 정렬할 숫자의 자릿수, b는 10
계수 정렬
각 숫자가 몇 개 있는지 개수를 세어 저장한 후 정렬하는 알고리즘

이미지 출처 : https://medium.com/@bill.shantang/8-classical-sorting-algorithms-d048eec3fdab
방법
- 정렬하고자 하는 배열의 최댓값을 구한다
- 최댓값 크기의 배열에 각 원소를 순회하며 해당 값이 몇 개인지 저장한다
- 저장된 데이터를 순서대로 출력한다
public int findMax(int[] arr) {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
return max;
}
public void countingSort(int[] arr) {
int[] sorted = new int[arr.length];
int max = findMax(arr);
int[] counting = new int[max + 1];
for (int i = 0; i < arr.length; i++) {
counting[arr[i]]++;
}
for (int i = 1; i < counting.length; i++) {
counting[i] += counting[i - 1];
}
for (int i = arr.length - 1; i >= 0; i--) {
counting[arr[i]]--;
sorted[counting[arr[i]]] = arr[i];
}
System.arraycopy(sorted, 0, arr, 0, arr.length);
}
시간 복잡도
- 평균 : O(n + k)
'공부 > 자료구조 | 알고리즘' 카테고리의 다른 글
| [자료구조] 이진탐색 (0) | 2024.02.05 |
|---|---|
| [자료구조] 해시 (1) | 2024.02.05 |
| [자료구조] 힙 (0) | 2024.01.26 |
| [자료구조] 그래프 (1) | 2024.01.26 |
| [자료구조] 트리 (0) | 2024.01.26 |